신호의 진폭(Amplitude)을 표현하는 방법이 몇가지 있다. 사인파형을 중심으로 진폭의 표현방법 4가지를 정리해봤다. 참고로, 아래의 내용들은 사인파 신호에 대해서 가장 이상적이고 깔끔하게 설명을 할 수 있긴 하지만, 그렇다고 다른 파형 신호들에 대해 적용할 수 없는 것은 아니다.
(1) 편진폭 (Single Amplitude, 0-peak)
사인파 신호의 중심선(0, zero)으로부터 신호의 최대값(마루, peak)까지의 거리를 말한다. 이 진폭을 표현하는 용어로는 편진폭, Single Amplitude, zero-to-peak 등의 있는데, 내가 생각할 때 가장 많이 쓰는 용어는 'zero-to-peak' 인 것 같다.

(2) 전진폭 (Double Amplitude, peak-peak)
전진폭은 사인파 신호 그래프에서 양(+)의 방향 최대값과 음(-)의 방향 최대값 간의 거리를 의미한다. 우리말로는 '마루' 에서 '골' 까지라고 할 수 있겠다. 이 진폭을 표현하는 용어로는 전진폭, Double Amplitude, peak-to-peak 등이 있는데, 그 중 'peak-to-peak' 이라는 용어를 가장 많이 쓰는 것 같다.

(3) RMS (Root Mean Square, 제곱평균제곱근)
RMS는 변동하는 진동신호의 진폭을 단일값으로 보여줄 수 있는 일종의 '대표값' 이다.
소음진동 시험 업무를 해보면, 여러개의 계측결과들을 두고 '어느것이 더 큰지' 서로 비교해야하는 상황이 자주 발생한다. 그러나, 일반적으로 소음이나 진동을 측정하여 얻는 신호는 시간에 따라 그 크기가 심하게 변동하는 '동적 신호(Dynamic Signal)' 이기 때문에, 비교결과 역시 시간에 따라서 달라지기 마련이다. 그래서, 각 측정결과를 대표할 수 있는 단일값으로 요약해서 비교를 해야 할텐데, 동적 신호의 속성을 어떤 하나의 단일값으로 요약한다는 것 또한... 무엇을 기준으로 잡아야 할지 판단하기 어려운 일이다.
아래 두 신호를 비교해보자. 둘 다 동시에 측정한 진동 신호이며, 동등하게 0~5 초까지의 신호를 샘플로 뽑았다고 가정해보자. A신호와 B 신호 중 어느 신호가 '더 큰지' 판단할 수 있을까?

언뜻 보기에 A신호의 peak 진폭이 더 큰 것처럼 보인다. 그렇지만 B신호는 진동이 더 밀도 높게 나타나는 것 같다. 어느 신호가 더 클까? 어떻게 판단해야 할까? 이런 경우, 가장 유용하면서도 가장 일반적으로 적용하는 '대표값' 이 바로 RMS 다. (※ 그렇다고 해서, Peak 값을 대표값으로 쓰지 않는 것은 아니다. 목적에 따라 Peak to Peak 값을 대표값으로 사용하는 경우도 있다. (ex. 변위 측정 등...))
각각의 RMS 값을 계산하면,
A신호 = 10.9
B신호 = 15.8
즉, B신호가 약 1.5배 크다고 할 수 있다.
RMS 계산은 어떻게 할까?
RMS는 Root Mean Squqre 의 약자로, '제곱 평균의 제곱근' 이다. 측정된 신호들(A₁, A₂, ...) 의 제곱의 합을 신호의 갯수(N)로 나누어 평균을 만든 뒤, 제곱근을 계산하는 방식이다.

우리가 측정하는 소음과 진동은 시간에 따라 변동하는 동적신호(Dynamic Signal) 이다. 다시말해, 측정을 위해 설정한 매 단위 시간마다 신호가 측정된다. 그래서 RMS 값은 계측 시간(T)에 대해 신호(x(t))의 제곱값의 평균을 구하는 과정이라고 보는게 더 맞겠다. RMS 값 계산식을 시간의 관점에서 다시 쓰면 다음과 같다.
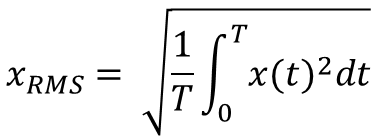
사인파 신호 (Sinusoidal Signal)에 한해서, 'RMS 값은 Peak 값의 0.707 배' 로 계산할 수 있다. (Peak 값을 2제곱근으로 나눈 것과 같음) 사인파 신호상에 Peak 값과 RMS 값을 비교하여 표시하면 아래 그림과 같다.

(4) 평균 (Average)
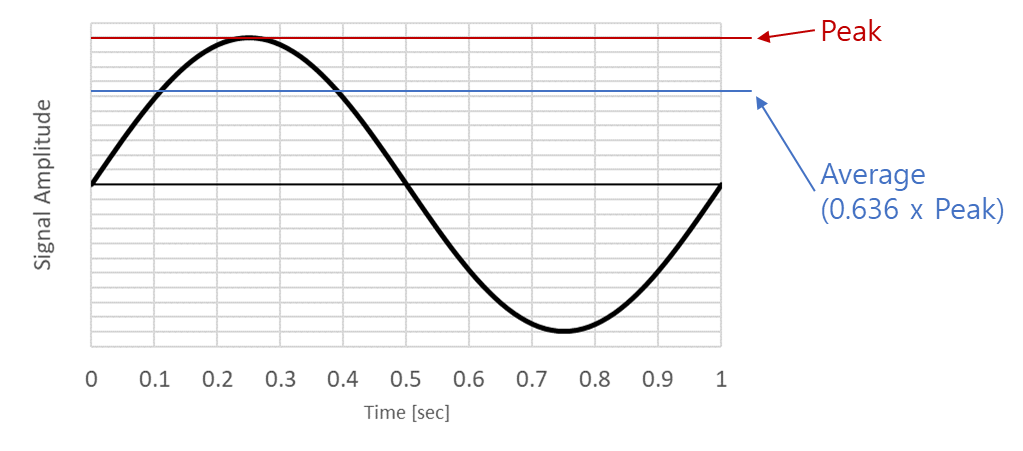
진폭을 표현하는 방법 4가지 중 마지막은 평균(Average)이다. RMS 값과 마찬가지로 평균값도 계측신호를 단일값으로 표현해주는 대표값 중 하나라고 할 수 있다. 평균값은 RMS값보다 조금 작다. 사인파 신호에 한해서, 평균값은 Peak 값의 0.636배로 단순계산할 수 있다.
끝.
'Study > Signal Analysis' 카테고리의 다른 글
| 사인파의 합성과 맥놀이(Beating) (0) | 2022.11.16 |
|---|---|
| 크레스트 팩터 (Crest Factor) (0) | 2022.11.12 |
| 주기(Time Period), 주파수(Frequency) (0) | 2022.11.05 |
| 주기성 신호의 종류 (0) | 2022.11.04 |
| 주기성 신호(Periodic Signal), 사인파 신호(Sinusoidal Signal) (0) | 2022.11.02 |