지금까지는 주기적 신호에 대해서 몇가지 글을 썼었다. 오늘은 비주기적 신호인 "랜덤 신호"에 대해서 간단히 정리해보려고 한다.
1. 랜덤 신호(Random Signal)란 무엇인가?
현상적 관점에서, 랜덤신호는 신호가 무작위적(Random)으로 나타나는 경우를 말하며, 신호의 형태나 특성 등이 반복되지 않는다(Not Repeatable). 그렇기에, 랜덤신호는 현재 신호의 값을 정확히 안다고 해도, 그 다음에 나타날 양상을 계산하거나 예측하는데에 전혀 도움이 되지 않는다.
조금 다르게 표현하면, 우리가 시간 t₁ 순간에서의 랜덤신호 값 x(t₁)을 정확하게 알고 있다고 하더라도, 그보다 시간이 약간 경과한 t₂ 순간에서의 랜덤신호값 x(t₂)를 계산하거나 예측할 수 없다는 의미다. 왜냐하면, 랜덤신호에서는 x(t₁) 과 x(t₂) 가 전혀 연관이 없고, 서로 독립적(Independent)이기 때문이다. (※ 이런 신호를 Non-deterministic Signal 이라고 하며, 대표적으로 Random Signal 이 있다.)
반면, 주기적신호인 sine파 신호의 경우, 시간 t₁ 순간에서의 sine파 신호값 x(t₁)을 정확히 알고 있다면, 시간 t₂ 순간에서의 sine파 신호값 x(t₂)을 정확히 알 수 있다. 왜냐하면 sine파 신호는 수식으로 명확하게 정의가 되어있고, 반복적으로 나타나기 때문이다. (※ 이런 신호를 Deterministic Signal 이라고 하며, 대표적으로 Periodic Signal 이 있다.)
랜덤신호는 일반적으로 다수의 독립적인 발생원들의 합성으로 구성되기 때문에, 주기적 신호인 sine파 신호처럼 간단한 수식으로 랜덤신호를 규정하고 표현할 수는 없다. 다만, 수학적으로 랜덤신호는 "통계적 방법(Stochastic Process)" 을 통해 표현할 수 있을 뿐이다. (※ Stochastic 은 좀 더 공부해서 다음 기회에 정리해봐야겠다.)
2. Periodic Signal 과 Random Signal의 비교
주기적 신호(Periodic Signal) 과 랜덤 신호(Random Signal) 의 차이를 직관적으로 볼 수 있게, 가상의 신호를 만들어 그래프를 그려봤다.
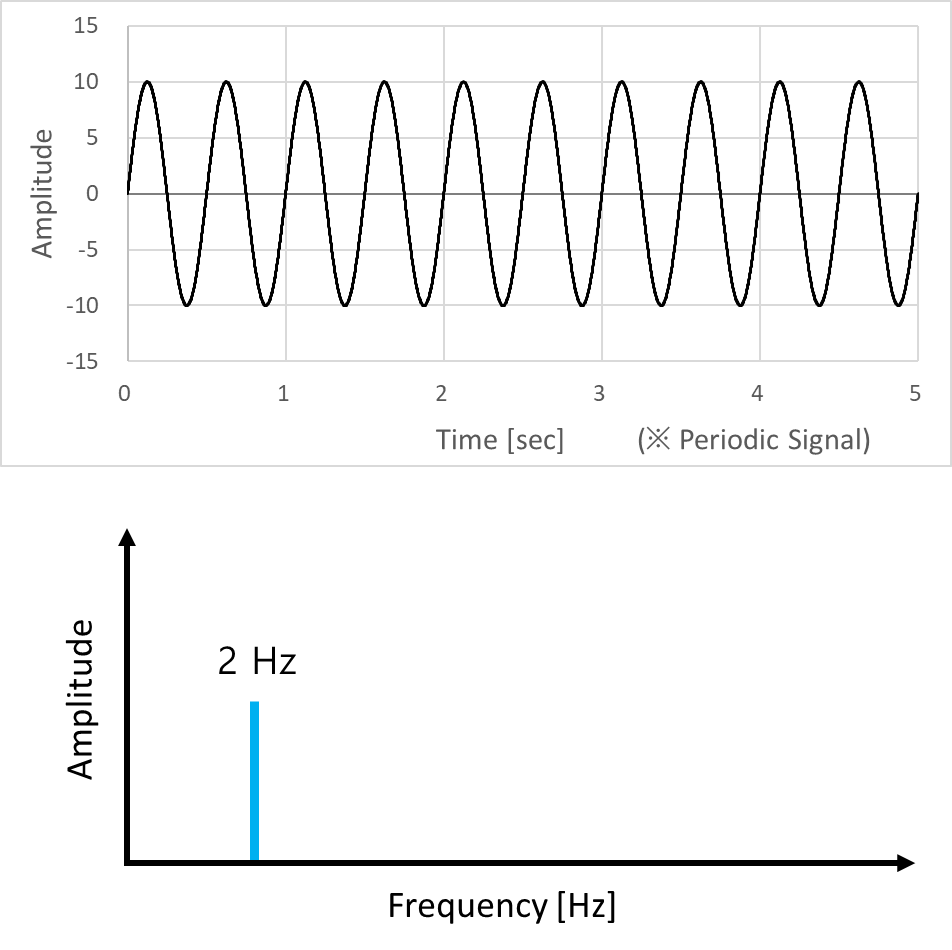
주기적 신호는 대표적으로 Sine파 신호를 가져와봤다. (※ 아래 그래프는 진폭 10, 주파수 2 Hz 의 Sine파 신호다.) Sine 파 신호의 반복적인 특성을 너무 잘 알기에, 1초 순간에서 진폭이 0 임을 알면 2초 순간에서도 진폭이 0 이 됨을 예측할 수 있다.
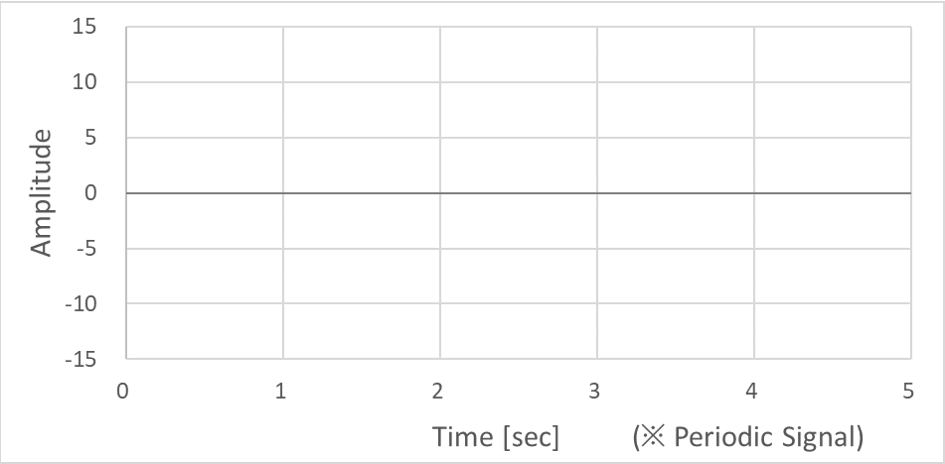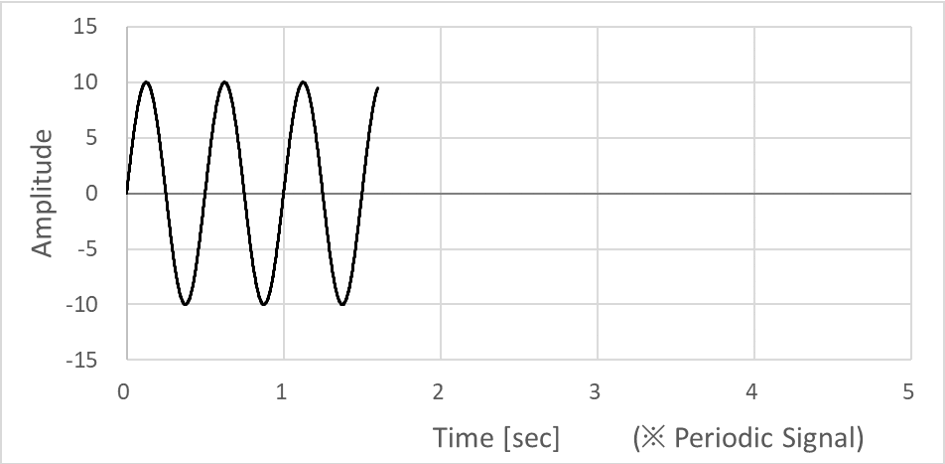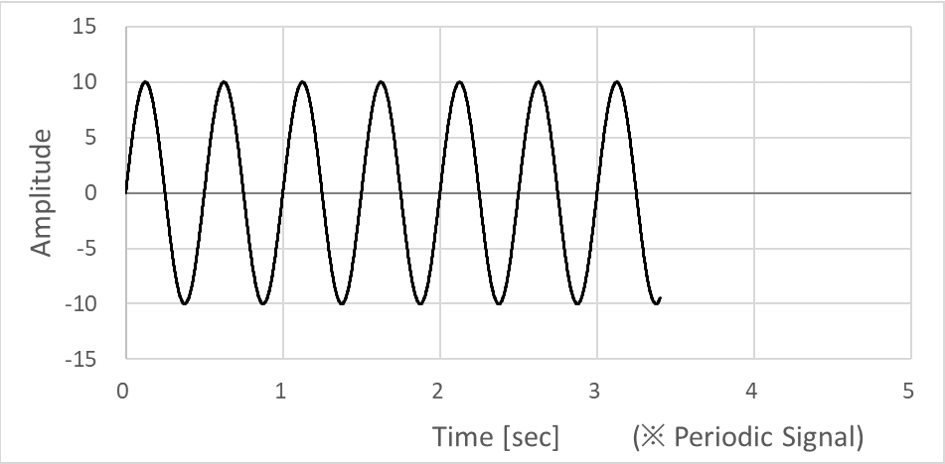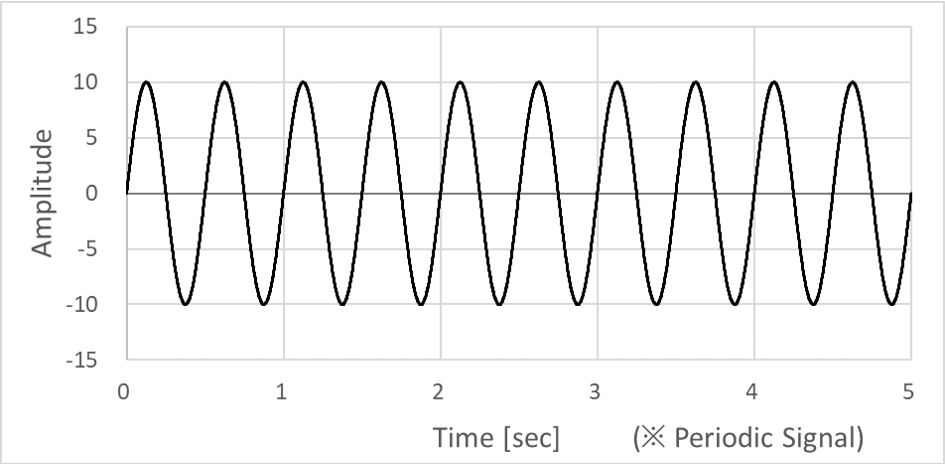
또한, Sine파 신호는 수학적으로 아래 식과 같이 정의할 수 있기 때문에, 1초, 2초와 같이 딱 떨어지는 시점이 아닌, 임의의 순간 t₁ , t₂ 에서도 그 값을 계산하고 예측할 수도 있다.


한편, 랜덤신호의 그래프를 보자.
1초 순간의 진폭을 안다고 해서, 2초 순간의 진폭을 알 수 있을까? 무언가... 예측이 불가능하겠다는 느낌이 든다. (예측할 수 없다.)

참고로 말하면, 이 랜덤신호에서 1초 순간의 진폭은 -1.81 이고, 2초 순간의 진폭은 -5.23 이더라. 규칙도 없고, 어떠한 연관성도 없다.

3. Random Signal 의 통계적 표현의 예
앞서, 랜덤신호는 통계적 방법으로 표현할 수 있다고 언급했는데, 그와 관련하여 간단한 예를 한가지 보려고 한다. 가장 보편적이고 단순한 통계적 표현방법 중 하나로 RMS (root mean square) 가 있다. (※ RMS 설명 글 링크)
먼저, sine파 신호 그래프에 1초단위로 RMS 값을 계산하여 파란색 선으로 표시하였다. 그래프를 통해서도 알 수 있지만, 이 신호에서 RMS = 7.07 로 일정하다. Peak 값이 10 이므로 당연히 RMS = 7.07 이기도 하다.

한편, 랜덤신호에서도 1초마다 RMS 값을 계산하여 초록색 선으로 표시하였다. 자세히 보면 각 초마다 RMS 값이 미세하게 달라진다. 하지만, 크게 보면 RMS 값이 거의 일정하게 나타나는 것을 볼 수 있다.

이 랜덤신호는 통계적으로(ex. RMS 값으로) 표현해봤을 때, 시간이 경과하여도 그 값이 거의 변하지 않고 일정한 수준을 유지하는 패턴(Pattern)을 보인다고 할 수 있다. 이런 유형의 랜덤신호를 특별히 Stationary Random Signal 이라고 부른다. 예를들어, 잘 포장된 아스팔트 도로 위를 "정속" 으로 주행하는 자동차에서 얻을 수 있는 진동신호가 Stationary Random Signal 에 가까울 것이다. (※ Stationary Random Signal 등 신호 분류 설명 글 링크)
Stationary Random Signal 은 일반적이지 않을 뿐더러, 그 마저도 장시간 관찰하면, 시간에 따라 변하는 상황이 오고야 만다. 결국 그냥 Random Signal 이 된다.
4. Random Signal 의 주파수
순수한 Sine파 신호는 이론적으로 딱 1개의 주파수만 갖고있다. 반면, 랜덤신호는 (관찰 범위 내) 모든 주파수를 갖고있다. (※ 언젠가 글을 쓸 기회가 있겠지만, 어쨌든, x축이 시간인 Time Domain Singal 을 → x축이 주파수인 Frequency Domain Spectra 로 표현하는 방법(Fourier Transform)이 있다.)
그래프로 보자.
순수 sine파 신호를 주파수 스펙트럼으로 표시하면, 아래 그림과 같이 1개 주파수만 뜬다.
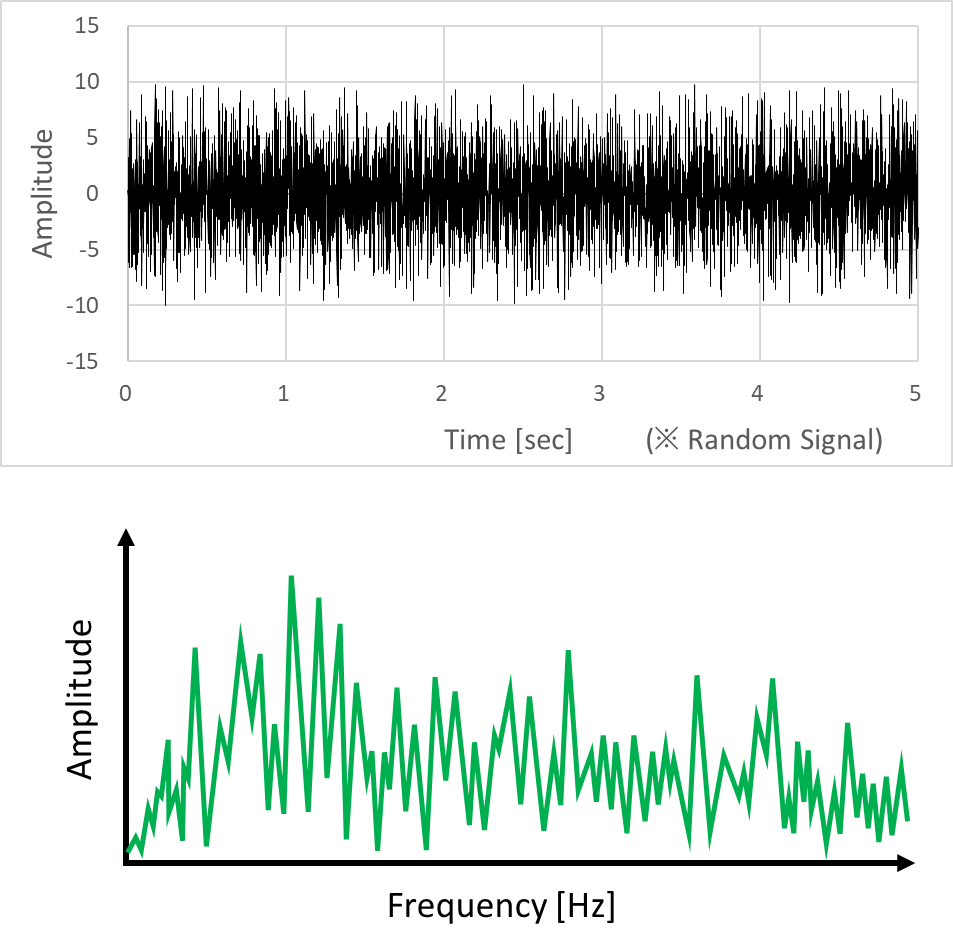
반면, 랜덤신호를 주파수 스펙트럼으로 표시하면, 아래 그림과 같이 모든 주파수에서 값을 가지고 있다. (※ 단, 설명을 위해 임의로 그린 파형이므로, 참고만 하자.)
끝.
'Study > Signal Analysis' 카테고리의 다른 글
| 선형 시스템 (Linear System) (0) | 2023.01.06 |
|---|---|
| 과도 신호 (Transient Signal) (0) | 2022.12.18 |
| 신호의 분류 방법 (Signal Classification) (0) | 2022.12.01 |
| 사인파의 합성과 위상차(Phase Difference) (0) | 2022.11.25 |
| 사인파 합성의 계산식 (0) | 2022.11.23 |