sine파의 합성은 어떻게 계산할까?
sine파 합성의 계산은 크게 두가지로 볼 수 있다.
(1) 더하기
(2) 곱하기
그런데, 사실 sine파의 "더하기" 와 "곱하기" 는 한 몸이라고 할 수 있다.
간단한 "계산식"을 통해 sine파의 합(+) 과 곱(×) 이 어떤 연관성을 갖고있는지 알아보고, 직관적인 이해를 위해서 "그래프"도 함께 살펴보고자 한다.
동일한 두 sine파 신호의 합(+) 계산
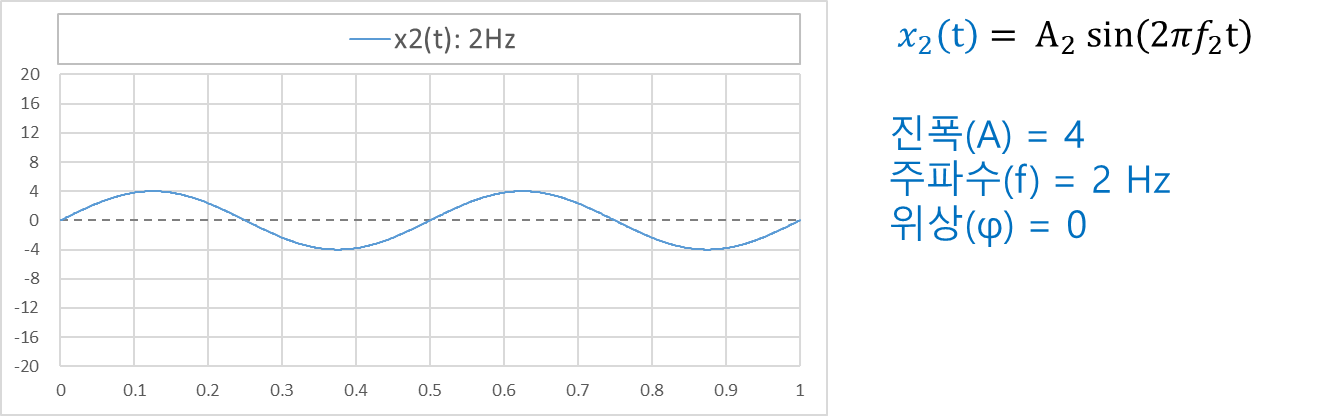
우선, 진폭 4, 주파수 2 Hz, 위상 0 인 두개의 동일한 sine파 신호를 만들어, x₁(t) 와 x₂(t) 라고 표시했다. (※ 계산의 편의를 위해 두 sine파 신호의 초기 위상(φ)은 '0' 으로 설정해둔다.)

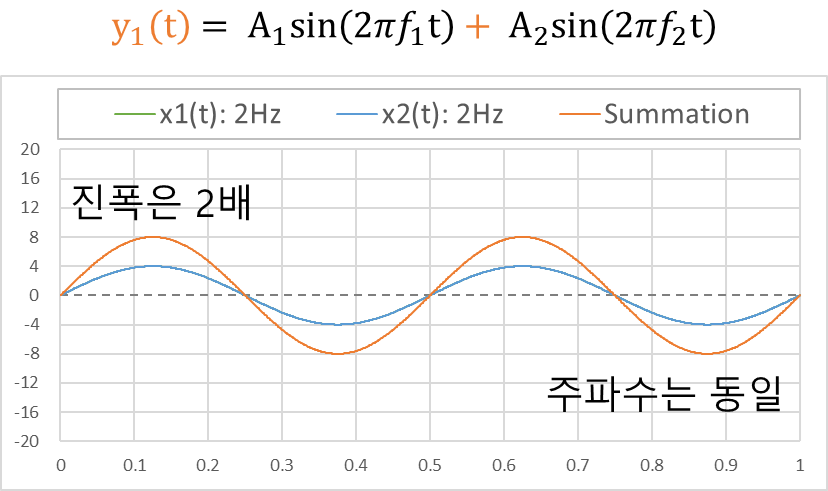
x₁(t) 와 x₂(t) 를 합(+) 한 신호인 y₁(t) 의 형상은 아래 그래프의 주황색 선과 같다. 합성된 파형의 진폭은 8, 주파수는 2 Hz 이다. 진폭은 2배가 되었고, 주파수는 동일하다.
이 상황을 계산식으로 나타내보자. sine파의 더하기는 고등학교때 배운 "삼각함수" 공식을 적용한다.
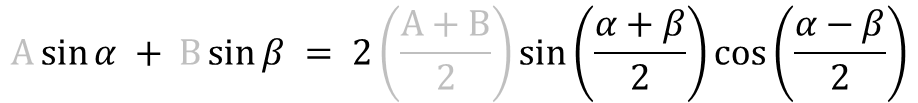
삼각함수 공식을 x₁(t) 와 x₂(t) 에 적용해보자.

두 sine파 신호가 서로 동일하다고 하였으므로, x₁(t) = x₂(t) 이고, A₁ = A₂ = A 및 f₁ = f₂ = f 라고 둘 수 있다. 그러면, 두 신호의 합(+)인 y₁(t) 은 다음과 같이 계산된다.

계산식도 그래프와 같은 결과를 나타낸다. 즉, 동일한 두 sine파를 합(+)하면 진폭은 2배가 되고, 주파수는 동일하다는 것을 알 수 있다.
sine파 신호의 합(+) 과 곱(×)의 관계
sine파 신호의 합(+) 과 곱(×) 의 관계를 알아본다.
앞서 소개한 계산식을 다시 불러와보자. 두 sine파를 합(+) 한 y₁(t) 는, 아래 식 처럼 (진폭) × (sine파) × (cosine파) 와 같이 곱(×) 으로 구성되는 것을 알 수 있다. (※ 참고 : sine파의 주파수 (f₁ + f₂)/2 는 두 주파수의 평균이고, cosine파의 주파수 (f₁ - f₂)/2 는 두 주파수 차의 절반이다.)
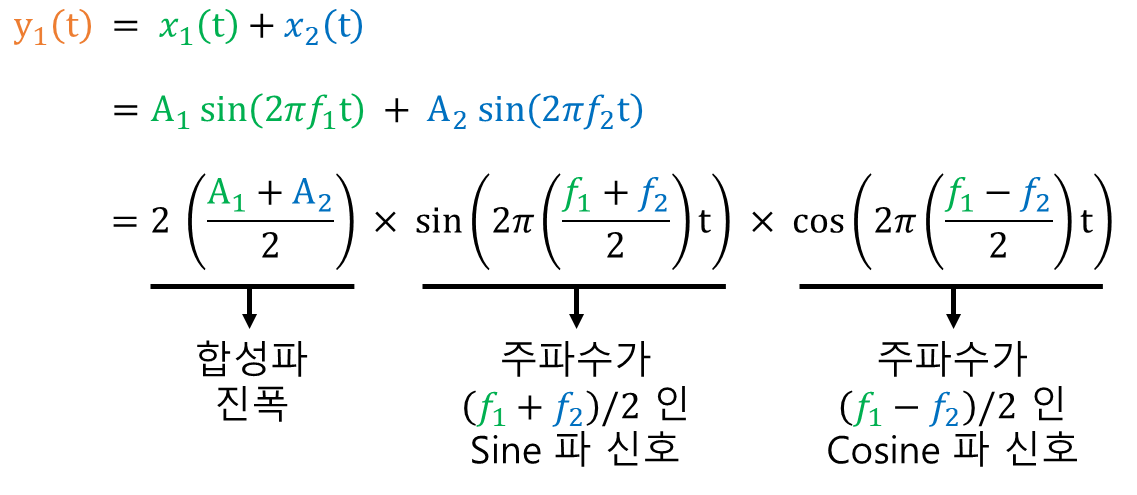
계산식으로부터 알 수 있듯이, sine파 신호의 합(+) 계산식은 → 곱(×) 계산식으로 나타낼 수 있다.
그래프로 그렸을 때에도, 합(+) 계산식과 곱(×) 계산식은 동일한 그래프를 나타낼까?
두 sine파 신호의 합(+) 계산식을 y₁(t) 라 하고, 곱(×) 계산식을 y₁(t) 라고 해보자. 그리고 각각의 그래프를 그려보면, 아래 그림과 같이 동일한 그래프가 얻어지는 것을 알 수 있다.
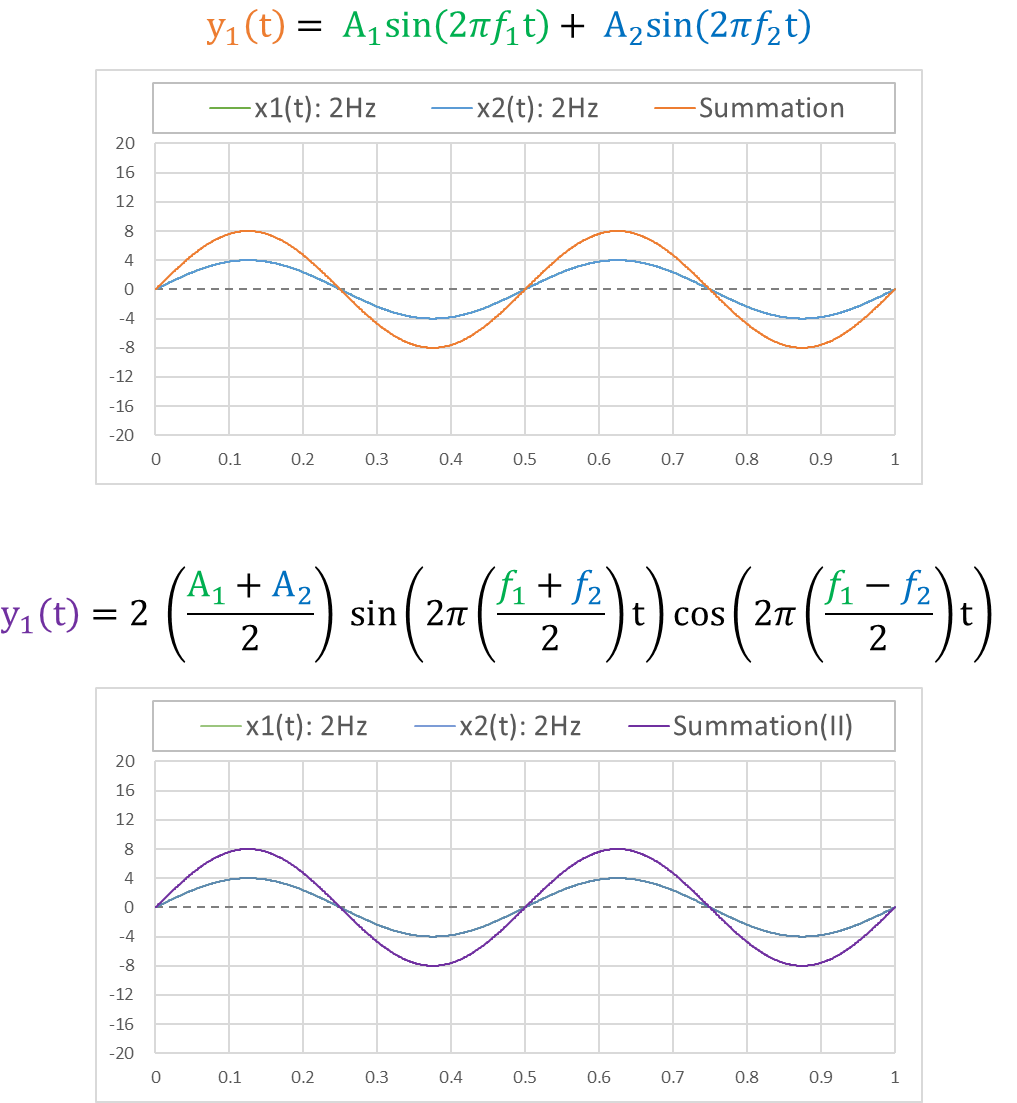
결론적으로, sine파 신호의 합성은 더하기와 곱하기로 나타낼 수 있고, 삼각함수 공식에 따라 두 sine파의 합(+)은 sine파와 cosine파의 곱(×)으로 나타낼 수 있다.
지금까지 설명한 것은 어디까지나 두 sine파의 위상(Phase)가 동일한 경우에만 해당한다. 위상의 변동은 두 sine파의 합성에 큰 영향을 미친다. 다음 글에서는 sine파의 합성이 위상에 따라 어떻게 변하는지 써봐야겠다.
끝.
'Study > Signal Analysis' 카테고리의 다른 글
| 신호의 분류 방법 (Signal Classification) (0) | 2022.12.01 |
|---|---|
| 사인파의 합성과 위상차(Phase Difference) (0) | 2022.11.25 |
| 사인파의 합성과 맥놀이(Beating) (0) | 2022.11.16 |
| 크레스트 팩터 (Crest Factor) (0) | 2022.11.12 |
| 진폭의 표현 방법 (Peak, RMS, 평균) (0) | 2022.11.05 |