기계진동 시스템과 관련된 여러 라플라스 변환쌍(Laplace Transform Pairs)들이 있다.
그 중에서도 「라플라스 영역에서의 곱(Multiplication)」과 「시간 영역에서의 합성곱(컨볼루전, Convolution)」간의 변환쌍이 특히 중요하다. (지금은 그냥 그렇구나... 하지만, 갈수록 중요해진다.)
1. 임펄스 응답과 합성곱
위 문장에서 곱셈(Multiplication)은 알겠는데, 합성곱(컨볼루전, Convolution)은 무엇일까?
설명을 위해서...
아래 그림과 같이, 시간 영역의 입력신호 x(t), 함수 h(t), 출력신호 y(t)로 구성된 시스템이 있다고 해보자.

이 시스템에서 합성곱의 수학적 정의는 다음과 같다. (※ 합성곱에 대한 자세한 내용은 다른 글에서 정리하겠음)

그러면, 「시간 영역의 합성곱」과 「라플라스 영역의 곱」이 서로 대응되는 라플라스 변환쌍은 아래와 같이 표현할 수 있다. 여기서 h(t)를 「임펄스 응답 (Impulse Response)」이라고 하고, h(t)는 라플라스 영역의 전달함수 H(s)를 역변환하여 얻을 수 있다.

임펄스 응답(Impulse Response) 이름의 뜻을 직역해보면, 어떤 시스템에 임펄스(Impulse)가 입력으로 작용했을 때, 출력으로서 얻어지는 응답(Response)이라고 할 수 있다.
그런데, 이 시스템의 출력은 분명히 y(t) 인데, 왜 h(t)도 출력 성격의 이름(임펄스 응답)을 붙여서 부르는 것일까?

사실, 그 이유는 입력신호 x(t)에서 찾을 수있다.
2. 임펄스 응답과 디랙 임펄스
h(t)를 임펄스 응답(Impulse Response)이라고 부르기 위한 조건이 하나 있다. 입력신호 x(t)가 이상적인 임펄스(Ideal Impulse)로 주어져야 한다.
이상적인 임펄스 입력신호를 「디랙 임펄스(Dirac Impulse)」라고 하며, δ(t)라고 쓴다. (※ 또는 디랙 델타(Dirac delta) 라고 부르기도한다.)
개념적으로, 디랙 임펄스는 발생시간이 무한히 짧고, 크기는 무한히 크다. 그래서 디랙 임펄스의 충격량은 1이며, 단위체(unity)로 많이 쓰인다. (그래서, 디랙 단위 임펄스(Dirac unit impulse) 라고도 부른다.)
중요한 점은, 디랙 임펄스의 라플라스 변환은 1로 정의된다는 것이다.

입력함수 x(t)가 디랙 임펄스 δ(t)로 들어온다면, 시간 영역의 합성곱을 아래와 같이 다시 쓸 수 있다.

그리고, 합성곱을 라플라스 변환 & 역변환하면, 아래와 같이 쓸 수 있다.

결국, 출력신호 y(t)는 이 시스템의 함수 h(t)와 같다는 결론이 나온다. h(t)를 출력 성격의 이름인 "임펄스 응답" 이라고 부르는 것은... 당연하다.
3. 결론 및 요약
시간영역 선형시스템에서 출력신호 y(t)는 입력신호 x(t)와 그 시스템의 함수 h(t)의 합성곱으로 표현할 수 있다.
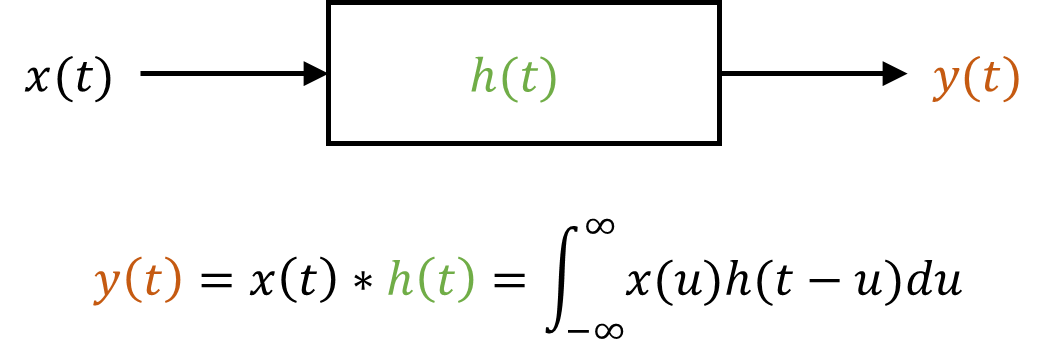
만약, 입력신호 x(t)가 디랙 임펄스(이상적인 임펄스) δ(t)이면, 출력 y(t)는 그 시스템의 함수 h(t)와 같아진다.
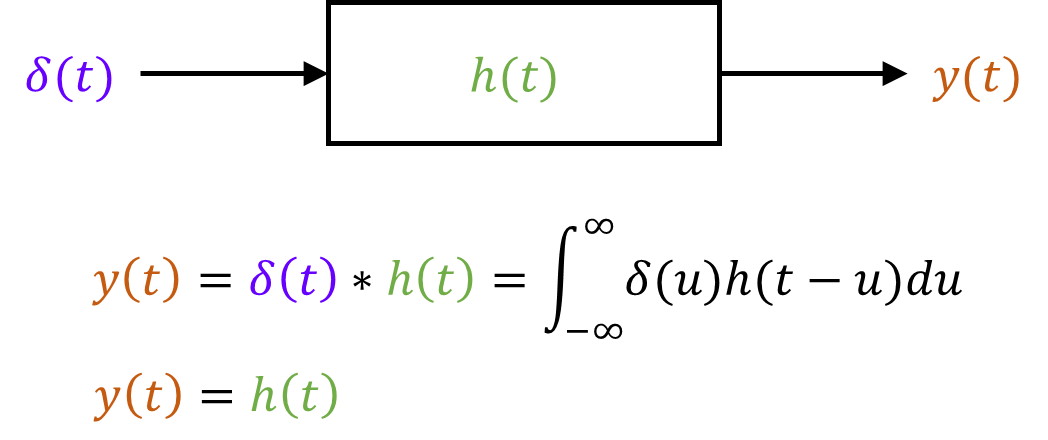
즉, 특정 조건(입력신호가 디랙 임펄스)에서는 시스템의 함수 h(t)가 그 시스템의 출력으로 주어질 수 있으며, 이때 h(t)를 임펄스 응답(Impulse Response)이라 부른다.
끝.
'Study > Signal Analysis' 카테고리의 다른 글
| 전달함수 (Transfer Function) (0) | 2023.06.23 |
|---|---|
| 라플라스 변환 (Laplace Transform) (0) | 2023.06.20 |
| 선형 시스템 (Linear System) (0) | 2023.01.06 |
| 과도 신호 (Transient Signal) (0) | 2022.12.18 |
| 랜덤 신호 (Random Signal) (0) | 2022.12.17 |